Hakikat Matematika dan Pembelajarannya di SD

Matematika merupakan salah satu bidang studi yang dijarkan di SD. Seorang guru SD yang akan mengajarkan matematika kepada siswanya, hendaklah mengetahui dan memahami objek yang akan diajarkannya, yaitu matematika.

Untuk menjawab pertanyaan “Apakah matematika itu ?” tidak dapat dengan mudah dijawab. Hal ini dikarenakan sampai saat ini belum ada kepastian mengenai pengertian matematika karena pengetahuan dan pandangan masing-masing dari para ahli yang berbeda-beda. Ada yang mengatakan bahwa matematika adalah ilmu tentang bilangan dan ruang, matematika merupakan bahasa simbol, matematika adalah bahasa numerik, matematika adalah ilmu yang abstrak dan deduktif, matematika adalah metode berpikir logis, matematika adalah ilmu yang mempelajari hubungan pola, bentuk dan struktur, matematika adalah ratunya ilmu dan juga menjadi pelayan ilmu yang lain.

Pengertian Matematika
Kata 'matematika' berasal dari perkataan Latin 'mathematika' yang mulanya diambil dari perkataan Yunani 'mathematike' yang berarti mempelajari. Perkataan itu mempunyai asal katanya 'mathema' yang berarti pengetahuan atau ilmu (knowledge, science). Kata 'mathematike' berhubungan pula dengan kata lainnya yang hampir sama, yaitu 'mathein' atau 'mathenein' yang artinya belajar (berpikir). Jadi, berdasarkan asal katanya, maka perkataan 'matematika' berarti ilmu pengetahuan yang didapat dengan berpikir (bernalar). Matematika lebih menekankan kegiatan dalam dunia rasio (penalaran), bukan menekankan dari hasil eksperimen atau hasil observasi matematika terbentuk karena pikiran-pikiran manusia, yang berhubungan dengan idea, proses, dan penalaran (Russeffendi ET, 1980 :148).

Matematika terbentuk dari pengalaman manusia dalam dunianya secara empiris. Kemudian pengalaman itu diproses di dalam dunia rasio, diolah secara analisis dengan penalaran di dalam struktur kognitif sehingga sampai terbentuk konsep-konsep matematika supaya konsep-konsep matematika yang terbentuk itu mudah dipahami oleh orang lain dan dapat dimanipulasi secara tepat, maka digunakan bahasa matematika atau notasi matematika yang bernilai global (universal). Konsep matematika didapat karena proses berpikir, karena itu logika adalah dasar terbentuknya matematika.

Pada awalnya cabang matematika yang ditemukan adalah Aritmatika atau Berhitung, Aljabar, Geometri setelah itu ditemukan Kalkulus, Statistika, Topologi, Aljabar Abstrak, Aljabar Linear, Himpunan, Geometri Linier, Analisis Vektor, dll.

Beberapa Definisi Para Ahli Mengenai Matematika antara lain :
☛ Russefendi (1988 : 23)
Matematika terorganisasikan dari unsur-unsur yang tidak didefinisikan, definisi-definisi, aksioma-aksioma, dan dalil-dalil di mana dalil-dalil setelah dibuktikan kebenarannya berlaku secara umum, karena itulah matematika sering disebut ilmu deduktif.

☛ James dan James (1976).
Matematika adalah ilmu tentang logika, mengenai bentuk, susunan, besaran, dan konsep-konsep yang berhubungan satu dengan lainnya. Matematika terbagi dalam tiga bagian besar yaitu aljabar, analisis dan geometri. Tetapi ada pendapat yang mengatakan bahwa
matematika terbagi menjadi empat bagian yaitu aritmatika, aljabar, geometris dan analisis dengan aritmatika mencakup teori bilangan dan statistika.

☛ Johnson dan Rising dalam Russefendi (1972)
Matematika adalah pola berpikir, pola mengorganisasikan,pembuktian yang logis, Matematika itu adalah bahasa yang menggunakan istilah yang didefinisikan dengan cermat, jelas dan akurat representasinya dengan simbol dan padat, lebih berupa bahasa simbol
mengenai ide daripada mengenai bunyi. Matematika adalah pengetahuan struktur yang terorganisasi, sifat-sifat dalam teori-teori dibuat secara deduktif berdasarkan kepada unsur yang tidak didefinisikan, aksioma, sifat atau teori yang telah dibuktikan kebenarannya adalah ilmu tentang keteraturan pola atau ide, dan Matematika itu adalah suatu seni, keindahannya terdapat pada keterurutan dan keharmonisannya.

☛ Reys - dkk (1984)
Matematika adalah telaahan tentang pola dan hubungan, suatu jalan atau pola berpikir, suatu seni, suatu bahasa dan suatu alat.

☛ Kline (1973)
Matematika itu bukan pengetahuan menyendiri yang dapat sempurna karena dirinya sendiri, tetapi adanya Matematika itu terutama untuk membantu manusia dalam memahami dan menguasai permasalahan sosial, ekonomi, dan alam.

Matematika adalah Ilmu Deduktif
Matematika dikenal sebagai ilmu deduktif, karena proses mencari kebenaran (generalisasi) dalam matematika berbeda dengan ilmu pengetahuan alam dan ilmu pengetahuan yang lain. Metode pencarian kebenaran yang dipakai adalah metode deduktif, tidak dapat dengan cara induktif. Pada ilmu pengetahuan alam adalah metode induktif dan eksperimen.
Walaupun dalam matematika mencari kebenaran itu dapat dimulai dengan cara induktif, tetapi seterusnya generalisasi yang benar untuk semua keadaan harus dapat dibuktikan dengan cara deduktif. Dalam matematika suatu generalisasi dari sifat, teori atau dalil itu dapat diterima kebenarannya sesudah dibuktikan secara deduktif.

Contoh dalam ilmu fisika, bila seorang melakukan percobaan (eksperimen) sebatang logam dipanaskan maka memuai dan dilanjutkan dengan logam-logam yang lainnya, dipanaskan ternyata memuai juga, maka ia dapat membuat kesimpulan (generalisasi) bahwa setiap logam yang dipanaskan itu dapat memuai. Generalisasi yang dibuat secara induktif tersebut dalam ilmu fisika dapat dibenarkan contoh dalam ilmu fisika di atas, pada matematika contoh-contoh seperti itu baru dianggap sebagai generalisasi jika kebenarannya dapat dibuktikan secara deduktif.

Berikut adalah beberapa contoh pembuktian dalil atau generalisasi pada matematika. Dalil atau generalisasi berikut dibenarkan dalam matematika karena sudah dapat dibuktikan secara deduktif.

Contoh 1:
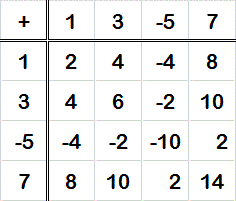
Bilangan ganjil ditambah bilangan ganjil adalah bilangan genap. Misalnya kita ambil beberapa buah bilangan ganjil, baik ganjil positif, atau ganjil negatif yaitu 1, 3, -5, 7.

Dari tabel disamping, terlihat bahwa untuk setiap dua bilangan ganjil jika dijumlahkan hasilnya selalu genap. Dalam matematika hasil di atas belum dianggap sebagai suatu generalisasi, walaupun anak membuat contoh-contoh dengan bilangan yang lebih banyak lagi. Pembuktian dengan cara induktif ini harus dibuktikan lagi dengan cara deduktif.

Pembuktian secara deduktif sebagai berikut :
Misalkan : a dan b adalah sembarang bilangan bulat, maka 2a bilangan genap dan 2b bilangan genap, maka 2a + 1 bilangan ganjil dan 2b + 1 bilangan ganjil.

Jika dijumlahkan:

(2a + 1) + (2b + 1)	= 2a + 1 + 2b + 1
	= 2a + 2b + 2
	= 2(a + b + 1)

Karena a dan b bilangan bulat maka (a + b + 1) juga bilangan bulat,
sehingga 2(a + b +1) adalah bilangan genap.
Jadi: bilangan ganjil + bilangan ganjil = bilangan genap (generalisasi)

Contoh 2:
Jumlah ketiga sudut dalam sebuah segitiga sama dengan 180°. Misalnya siswa mengukur ketiga sudut sebuah segitiga dengan busur derajat dan menjumlahkan ketiga sudut tersebut, ternyata hasilnya sama dengan 180°. Walaupun proses pengukuran dan penjumlahan ketiga sudut ini diberlakukan kepada segitiga-segitiga yang lain dan hasilnya selalu sama dengan 180°, tetap kita tidak dapat menyimpulkan bahwa jumlah ketiga sudut dalam sebuah segitiga sama dengan 180°, sebelum membuktikan secara deduktif.
Pembuktian secara deduktif sebagai berikut:

Garis a // garis b, dipotong oleh garis c dan garis d, maka terbentuk $ \angle _{1}, \angle _{2}, \angle _{3}, \angle _{4}, \angle _{5}, \angle _{6}$
➊ $ \angle _{1} + \angle _{2} + \angle _{6} = 180^{\circ} $ (membentuk sudut lurus)
➋ $ \angle _{1} = \angle _{5} $ (dua sudut yang saling bertolak belakang)
➌ $ \angle _{2} = \angle _{4} $ (dua sudut yang saling bertolak belakang)
dari persamaan ➊, ➋, ➌ diperoleh: $ \angle _{1} + \angle _{2} + \angle _{6} = \angle _{5} + \angle _{4} + \angle _{6} = 180^{\circ} $
Karena: $ \angle _{4} + \angle _{5} + \angle _{6}$ merupakan Jumlah dari ketiga buah sudut pada sebuah segitiga, maka dapat disimpulkan bahwa jumlah ketiga sudut dalam sebuah segitiga sama dengan 180°.

Kesimpulan yang didapat dengan cara deduktif ini barulah dapat dikatakan dalil atau generalisasi. Dalil-dalil dan rumus matematika itu ditentukan secara induktif (eksperimen), tetapi begitu suatu dalil ditemukan maka generalisasi itu harus dibuktikan kebenarannya secara deduktif.

Pada pembelajaran matematika di SD pembuktian dengan cara deduktif masih sulit dilaksanakan. Karena itu siswa SD hanya melakukan eksperimen (metode induktif). Percobaan-percobaan inipun masih menggunakan benda-benda konkrit (nyata). Untuk pembuktian deduktif
masih sulit dilaksanakan karena pembuktian deduktif lebih abstrak dan menuntut siswa mempunyai pengetahuan-pengetahuan siswa yang sebelumnya. Contoh : Pada pembuktian bilangan ganjil ditambah ganjil sama dengan bilangan genap siswa harus sudah mengerti bilangan ganjil, genap, bulat dan dapat menyelesaikan dalam bentuk umum bilangan-bilangan tersebut.

Matematika Adalah Ilmu Terstruktur
Matematika merupakan ilmu terstruktur yang terorganisasikan. Hal ini karena matematika dimulai dari unsur yang tidak didefinisikan, kemudian unsur yang didefinisikan ke aksioma/postulat dan akhirnya pada teorema. Konsep-konsep matematika tersusun secara hierarkis, terstruktur, logis, dan sistimatis mulai dari konsep yang paling sederhana sampai pada konsep yang paling kompleks. Oleh karena itu untuk mempelajari matematika, konsep sebelumnya yang menjadi prasyarat, harus benar-benar dikuasai agar dapat memahami topik atau konsep selanjutnya.

Dalam pembelajaran matematika guru seharusnya menyiapkan kondisi siswanya agar mampu menguasai konsep-konsep yang akan dipelajari mulai dari yang sederhana sampai yang lebih kompleks.

Contoh seorang siswa yang akan mempelajari sebuah volume kerucut haruslah mempelajari mulai dari lingkaran, luas lingkaran, bangun ruang dan akhirnya volume kerucut. Untuk dapat mempelajari topik volume balok, maka siswa harus mempelajari rusuk/garis, titik sudut, sudut, bidang datar persegi dan persegi panjang, luas persegi dan persegi panjang, dan akhirnya volume balok.

Struktur matematika adalah sebagai berikut:
Ⓐ Unsur-unsur yang tidak didefinisikan
Misal : titik, garis, lengkungan, bidang, bilangan dll.
Unsur-unsur ini ada, tetapi kita tidak dapat mendefinisikannya.

Ⓑ Unsur-unsur yang didefinisikan
Dari unsur-unsur yang tidak didefinisikan maka terbentuk unsur-unsur yang didefinisikan.
Misal : sudut, persegi panjang, segitiga, balok, lengkungan tertutup sederhana, bilangan ganjil, pecahan desimal, FPB dan KPK dll.

Ⓒ Aksioma dan postulat
Dari unsur-unsur yang tidak didefinisikan dan unsur-unsur yang didefinisikan dapat dibuat asumsi-asumsi yang dikenal dengan aksioma atau postulat.
Misal :
✓ Melalui 2 titik sembarang hanya dapat dibuat sebuah garis.
✓ Semua sudut siku-siku satu dengan lainnya sama besar.
✓ Melalui sebuah titik hanya dapat dibuat sebuah garis yang tegak lurus ke sebuah garis yang lain.
✓ Sebuah segitiga tumpul hanya mempunyai sebuah sudut yang lebih besar dari 90°.
Aksioma tidak perlu dibuktikan kebenarannya tetapi dapat diterima kebenarannya berdasarkan pemikiran yang logis.

Ⓓ Dalil atau Teorema
Dari unsur-unsur yang tidak didefinisikan dan aksioma maka disusun teorema-teorema atau dalil-dalil yang kebenarannya harus dibuktikan dengan cara deduktif.
Misal :
✈ Jumlah 2 bilangan ganjil adalah genap
✈ Jumlah ketiga sudut pada sebuah segitiga sama dengan 180°
✈ Jumlah kuadrat sisi siku-siku pada sebuah segitiga siku-siku sama dengan Kuadrat sisi miringnya.

Matematika Adalah Ilmu Tentang Pola dan Hubungan
Matematika disebut sebagai ilmu tentang pola karena pada matematika sering dicari keseragaman seperti keterurutan, keterkaitan pola dari sekumpulan konsep-konsep tertentu atau model yang merupakan representasinya untuk membuat generalisasi.
Misal :
jumlah a bilangan ganjil positif berurutan dari yang pertama sama dengan a²
Contoh :
➀ a=1 ⇒ jumlahnya 1²=1
➁ a=2 yaitu 1 dan 3 ⇒ jumlahnya adalah 2²=4
➂ a=3 yaitu 1, 3, dan 5 ⇒ jumlahnya adalah 3²=9
➃ a=4 yaitu 1, 3, 5, dan 7 ⇒ jumlahnya adalah 4²=16. . . dan seterusnya

Dari contoh-contoh tersebut, maka dapat dibuat generalisasi yang berupa pola yaitu:
"jumlah a bilangan ganjil positif berurutan dari yang pertama sama dengan a²"

Matematika disebut ilmu tentang hubungan karena konsep matematika satu dengan lainnya saling berhubungan.
Misalnya :
Antara persegi panjang dengan balok, antara persegi dengan kubus, antara kerucut dengan lingkaran, antara 5×6 = 30 dengan 30 : 5 = 6, antara 10² =100 dengan √100 = 10.
Demikian juga cabang matematika satu dengan lainnya saling berhubungan seperti aritmatika, aljabar, geometri dan statistika, dan analisis.

Matematika Adalah Bahasa Simbol
Matematika yang terdiri dari simbol-simbol yang sangat padat arti dan bersifat internasional. Padat arti berarti simbol-simbol matematika ditulis dengan cara singkat tetapi mempunyai arti yang luas.
Misal:
$ \sqrt{9}=3,\ 3+5=8,\ 3!=3\cdot 2\cdot 1 $

$ log\ 100\ =2,\ \lim_{x\rightarrow 3} 2x\ =\ 6 $

$ \frac{\partial y}{\partial x}. \ sin\ x. \ cos\ x. \ tan\ x. \leftarrow. \leftrightarrow. >. <. \cup. \cap. \forall. \therefore\ dan\ sebagainya $

Matematika sebagai Ratu dan Pelayan Ilmu
Matematika sebagai ratu ilmu artinya matematika sebagai alat dan pelayan ilmu yang lain.

Kegunaan Matematika
1. Matematika sebagai pelayan ilmu yang lain.
Banyak ilmu-ilmu yang penemuan dan pengembangannya bergantung dari matematika.
Contoh :
➲ Penemuan dan pengembangan Teori Mendel dalam Biologi melalui konsep Probabilitas.
➲ Perhitungan dengan bilangan imajiner digunakan untuk memecahkan masalah tentang kelistrikan.
➲ Dengan matematika, Einstein membuat rumus yang dapat digunakan untuk menaksir jumlah energi yang dapat diperoleh dari ledakan atom.
➲ Dalam ilmu pendidikan dan psikologi, khususnya dalam teori belajar, selain digunakan statistik juga digunakan persamaan matematis untuk menyajikan teori atau model dari penelitian
➲ Dalam ilmu kependudukan, matematika digunakan untuk memprediksi jumlah penduduk dll.
➲ Dalam seni grafis, konsep transformasi geometric digunakan untuk melukis mosaik.
➲ Dalam seni musik, barisan bilangan digunakan untuk merancang alat musik.
➲ Banyak teori-teori dari Fisika dan Kimia (modern) yang ditemukan dan dikembangkan melalui konsep Kalkulus.
➲ Teori Ekonomi mengenai Permintaan dan Penawaran dikembangkan melalui konsep Fungsi Kalkulus tentang Diferensial dan Integral.

2. Matematika digunakan manusia untuk memecahkan masalahnya dalam kehidupan sehari-hari.
Contoh :
➲ Memecahkan persoalan dunia nyata
➲ Mengadakan transaksi jual beli, maka manusia memerlukan proses perhitungan matematika yang berkaitan dengan bilangan dan operasi hitungnya
➲ Menghitung luas daerah
➲ Menghitung jarak yang ditempuh dari suatu tempat ke tempat yang lain
➲ Menghitung laju kecepatan kendaraan
➲ Membentuk pola pikir menjadi pola pikir matematis, orang yang mempelajarinya kritis, sistimatis dan logis.
➲ Menggunakan perhitungan matematika baik dalam pertanian, perikanan, perdagangan, dan perindustrian.

=============
Hakikat Matematika dan Pembelajaran Matematika SD

• ➨ Pendahuluan
  
• ➨ Kegiatan Belajar 1
  Hakikat Matematika, yang mencakup pengertian matematika, beberapa pendapat dari para ahli mengenai matematika, matematika adalah ilmu deduktif, ilmu terstruktur, ilmu tentang pola dan hubungan, matematika adalah bahasa simbol dan kegunaan matematika.
  
• ➨ Kegiatan Belajar 2
  Hakikat Anak Didik yang mencakup anak sebagai suatu individu dan anak usia SD dalam pembelajaran matematika di SD, meningkatkan minat belajar matematika pada anak dan upaya peningkatan prestasi anak dalam pembelajaran matematika.
  
• ➨ Kegiatan Belajar 3
  Pembelajaran Matematika di SD yang mencakup ciri-ciri pembelajaran matematika di SD, yaitu pembelajaran matematika menggunakan pendekatan spiral, pembelajaran matematika bertahap, pembelajaran matematika menggunakan pendekatan indukktif, pembelajaran matematika kebenaran konsisten, dan pembelajaran matematika hendaknya bermakna.

DAFTAR PUSTAKA

• Andi Hakim, N. (1980). Landasan Matematika, Jakarta : Bharata Aksara.
• Erman, S dan Winataputra, U.S. (1993). Strategi Belajar Mengajar Matematika, Jakarta : Universitas Terbuka.
• Herman, H. (1990). Strategi Belajar Matematika, Malang : IKIP Malang.
• Lisnawaty, S. (1992). Metode Mengajar Matematika 1, Jakarta : PT. Rineka Cipta
• Ruseffendi, E.T. (1988). Pengajaran Matematika Modern dan Masa Kini Untuk Guru dan SPG, Bandung : Tarsito.
• Ruseffendi, E.T. (1988). Pengantar Kepada Membantu Guru Mengembangkan Kompetensinya dalam Pengajaran Matematika Untuk Meningkatkan CBSA, Bandung : Tarsito.
• Ruseffendi, E.T, dkk. (1992), Pendidikan Matematika 3, Jakarta : Depdikbud.
• Wragg, E.C. (1997). Keterampilan Mengajar Di Sekolah Dasar, Jakarta : Gramedia

Mengerjakan pembagian pecahan umumnya kita harus kembalikan ke perkalian pecahan, lihat pada video ini dikerjakan dengan cara pilar (pintar bernalar);

Sumber https://www.defantri.com/

Share this post