Geometri: Alat Peraga Rangka Bangun Ruang Terbuat Dari Kertas

Banyak cara mengubah kertas menjadi lebih bernilai daripada kertas itu dibuang lalu dibakar. Kali ini kita coba berbagi informasi tentang membuat alat peraga dari kertas, kertas yang digunakan adalah semua jenis kertas yang tipis seperti kertas koran atau buku. Disini diambil sebagai contoh adalah kertas koran karena dapat menghasilkan ukuran yang lebih panjang dari kertas buku. Bagaimana cara membuatnya,... sabar... kita cerita sedikit tentang alat peraga.

Dalam proses belajar mengajar menggunakan alat bantu seperti alat peraga sudah pasti memberikan nilai tambah dalam proses belajar dan peserta didik akan lebih memperhatikan jika kita gunakan media lain selain buku teks dalam proses belajar. Terkhusus dalam topik bangun ruang atau dimensi-3 kesulitan peserta didik lebih dominan adalah membayangkan bangun ruang tersebut lalu di bangun ruang tersebut terdapat bidang-bidang atau garis yang mempunyai kedudukan tersendiri.

Alat bantu pada di topik dimensi tiga ini dapat menggunakan program geogebra di komputer Anda tetapi jika infokus masih barang langka di Sekolah Anda maka alat peraga dari kertas ini akan sangat membantu.

Sebagai contoh kita ambil soal Ujian Nasional IPA tahun 2007:
Diketahui sebuah kubus ABCD.EFGH dengan panjang rusuk $ 6\sqrt{3} $, jarak bidang $ACH$ dan $EGB$ adalah...
$\begin{align}
(A)\ & 4\sqrt{3}\ cm \\

(B)\ & 2\sqrt{3}\ cm \\
(C)\ & 4\ cm \\
(D)\ & 6\ cm \\
(E)\ & 12\ cm
\end{align}$
Penyelesaian:
Dalam menyelesaiakan permasalahan tentang bangun ruang, kemampuan dasar yang harus kita miliki adalah mampu menggambarkan bangun ruang tersebut. Disini gambar yang ditampilkan adalah gambar dengan menggunakan program geogebra dan dengan bantuan alat peraga.

Sekarang coba kita gambar bidang bidang ACH dan EGB di kubus ABCD.EFGH

Jika kita perhatikan gambar diatas dengan dua kubus yang dibangun dengan objek yang berbeda, keduanya mempunyai kelebihan dan kekurangan. Setelah memperhatikan bidang $ACH$ dan $EGB$ di kubus $ABCD.EFGH$, agar melihat bidang ada namanya perhatikan gambar kanan, kita akan lihat kedudukan bidang $ACH$ dan $EGB$ adalah sejajar berarti bidang tersebut mempunyai jarak.

Coba kita lihat kubus tepat dari sisi bidang diagonal atau perhatikan segi empat $BDHF$, kita akan melihat sebuah persegi panjang seperti gambar di atas. Bidang $ACH$ (biru) kita lihat dari samping sehingga menjadi berupa garis (biru) begitu juga dengan bidang $EGB$ (hijau) menjadi berupa garis (hijau). Dari gambar yang menjadi jarak bidang $ACH$ dan $EGB$ adalah $KL$, sekarang tugas kita adalah mengitung panjang $KL$.
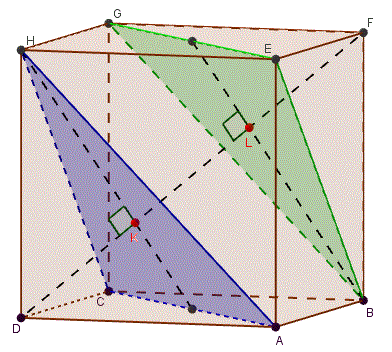
$\begin{align}
DF &= \text{Diagonal Ruang} \\
&= \text{Panjang rusuk} \cdot \sqrt{3} \\
&= 6 \sqrt{3} \cdot \sqrt{3} \\
& = 6\sqrt{9} \\
&= 6\cdot 3 \\
&= 18 \\
\hline
KL &= \frac{1}{3}DF \\
&= \frac{1}{3} \cdot 18 \\
&= 6
\end{align}$

Jarak bidang $ACH$ dan $EGB$ adalah $6\ cm$

Berdasarkan pengamatan sehari-hari siswa belum bisa terima kalau $DK=KL=FL$, sehingga kita ambil alternatif penyelesaian. Perhatikan $\bigtriangleup MDH \cong \bigtriangleup BFN$ sehingga $DK=FL$ karena $DK$ dan $FL$ merupakan tinggi masing-masing segitiga pada posisi yang sama. Dari $\bigtriangleup MDH$ kita peroleh persamaan:
$\begin{align}
MH \cdot DK &= \ MD \cdot DH \\
DK &= \frac{MD \cdot DH}{MH} \\
&= \frac{3\sqrt{6} \cdot 6\sqrt{3}}{3\sqrt{18}} \\
&= \frac{18\sqrt{18}}{3\sqrt{18}} \\
&= 6 \\
\hline
DF &= DK + KL + FL \\
18 &= 6 + KL + 6 \\
KL &= 18 - 12 \\
KL &= 6
\end{align}$
Mungkin itu sebagai salah satu contoh pembahasan soal Ujian Nasional tentang jarak dua bidang sejajar dan pembahasan soal sebelumnya dari siswa yaitu jarak titik ke bidang.

Sekarang kita lihat bagaimana pembuatan alat peraga dari kertas tersebut.
Langkah awalnya adalah cari kertas koran, edisi hari ini atau kemarin juga boleh dan jangan mimpi dapat koran edisi besok. Setelah dapat korannya lalu baca, kalau Anda belum tahu apa yang mau dikerjakan berikutnya karena akan lebih asyik nunggu langkah berikutnya sambil baca koran dari pada sambil bahas soal seperti yang diatas.

Langkah kedua adalah dengan menggulung kertas koran tersebut sampai gulungan mempunyai diameter yang Anda rasa sudah cukup, sewaktu menggulung kertas pastikan tidak ada ruang diantara kertas. Setelah kertas koran selesai digulung lalu beri lem digulungan terakhir agar kertas tidak terbuka lagi dan buatlah beberapa buah.

Langkah berikutnya, untuk tahap belajar kita membangun rangka kubus jadi kita perlu 12 gulungan kertas yang ukurannya sama. Lalu gabung gulungan kertas menjadi rangka kubus dan rekatkan dengan menggunakan lem yang kualitasnya baik agar rangka bangun ruang yang Anda bangun tidak lepas.

Di kelas X kita akan bertemu dengan topik jarak titik-garis-bidang dan sudut garis-bidang seperti contoh soal diatas, untuk membuat garis baru agar lebih mudah cukup gunakan lidi yang lurus seperti gambar diatas.

Secara khusus diucapkan terimakasih kepada Petrus Septo Pardede siswa SMA Negeri 2 Lintongnihuta angkatan I dan kawan-kawanya karena dengan bantuan mereka alat peraga ini dapat cepat selesai dan dapat dipergunakan.

Semoga bermanfaat dan dapat dipergunakan untuk kemajuan Pendidikan di Indonesia. Saran dan kritikan untuk alat peraga yang kami buat ini sangat kami harapkan, terima kasih😊CMIIW

Jangan Lupa Untuk Berbagi 🙏Share is Caring 👀 dan JADIKAN HARI INI LUAR BIASA! - WITH GOD ALL THINGS ARE POSSIBLE😊

Mengerjakan pembagian pecahan umumnya kita harus kembalikan ke perkalian pecahan, lihat pada video ini dikerjakan dengan sangat kreatif;

Sumber https://www.defantri.com/

Share this post